A Theoretical and Empirical Analysis of Everlasting Options
Motivation
For most people Friday is one of the best days of the week — the weekend is ahead with time to relax and enjoy. However, for those in the crypto options market-making business, Friday at 8:00am UTC is perhaps the most intense moment for the entire week. This is when major maturities such as the weekly, monthly, and quarterly options expire.
Why is this such a big deal?
Market-makers generally like to stay delta-neutral, meaning they hedge their positions in such a way that they won’t make or lose money if the price of the underlier moves by a small amount. This is because they generally don’t have an opinion about changes in the underlying asset price, and don’t want to be exposed to the risk of it changing. Because the instruments market-makers use to stay delta neutral generally don’t expire, while the options themselves do, when options expire on Friday, this results in a significant change to the overall delta exposure for the entire portfolio. Let’s consider an example for BTC Deribit options which are cash-settled:
- Suppose it’s several hours before expiry and the market-maker has +100 BTC call options in their inventory.
- Let's say the delta for each individual call is +0.99 which means for a +1.00% change in BTC, the underlying call should theoretically move by +0.99%.
- The market-maker has an options delta exposure of +99 BTC (0.99 x 100) and will be short 99 BTC worth of the underlying futures to ensure a flat delta profile (0 delta exposure).
Now suppose a few hours pass and the options expire in the money. This will completely change the delta exposure of the market-maker’s portfolio:
- Initial delta exposure: +99 BTC (options) - 99 BTC (futures) = 0 BTC
- Post options expiry delta exposure: -99 BTC (futures)
Right after the expiry, the market-maker is left with a massive delta exposure to the futures but no offsetting exposure in the options. Most market-makers will anticipate this in advance and calculate their post expiry delta exposure to hedge their book accordingly. Nevertheless, they will still have to constantly monitor their post expiration risk and prepare their hedging plan in advance. Even option traders who want to make directional bets must carefully roll their positions into new maturities once they expire. Overall, in either case, the fact that options expire in the first place is the root cause for this intense monitoring — the wrong trade could lead to disastrous consequences.
A Potential Solution
Inspired by the wildly successful cryptocurrency perpetual futures product, Dave White and Sam Bankman-Fried proposed a new way to think about trading options. An everlasting option has similar characteristics to a normal option but it can be traded like a perpetual futures contract such that it doesn’t expire. Instead of a trader having to constantly roll their options after each expiry, they could simply trade an everlasting option and maintain perpetual exposure to the option.
An everlasting option can be replicated with a basket of options with different maturities. In the original paper each option was weighted in an exponentially weighted arithmetic manner (ie: first option = 50%, second option = 25%, third option = 12.5% etc…) which makes its replication relatively simple.
Similar to perpetual futures contracts, an everlasting option has a funding fee which needs to be paid on a recurring basis. In our analysis, the funding fee will be paid on a daily basis and is calculated as the difference between the everlasting option price (before funding) and everlasting option payoff.
Let’s consider an example adapted from the paper:
- Suppose BTC is trading at $35k and a trader has bought a $34k strike everlasting call option. At this time the payoff of the everlasting call option is $1k (spot - strike).
- Furthermore, let’s say the everlasting call option was trading at $1.2k before funding was paid. At the time of funding the longs would pay the shorts $200.
- In this example we’re looking at the case where funding is paid on a daily basis but the frequency can be adjusted to match whichever time horizon.
Note: while this product may appear similar to an American perpetual option, the everlasting option doesn’t require any payment up front, just like a perpetual futures contract.
For the remainder of this article we’ll focus on how this product can be traded in real-world markets. We’ll start off by constructing everlasting option prices using raw Deribit historical option data. From there we’ll also look into the theoretical greek and price behaviour for this option. For anyone interested in analyzing the code you can follow along here.
Part 1: Analysis Using Historical Options Data
The goal with this analysis is to construct the historical price of an everlasting option using real-world Deribit data. With this analysis we can understand how this option trades relative to the underlying price. This example will focus on pricing a $50k BTC everlasting call option with two months of daily BTC options price history.
A. Data Cleaning and Preparation
- For each day we will record the USD price of the Deribit BTC $50k call option across all maturities into a CSV file. As an example, the data on 2021-03-03 lists the $50k call option prices across 10 different maturities.
- One of the limitations with this current data is that the maturities are not continuously spaced between each maturity. The data on 2021-03-03 has only 10 option maturities, however, in order to accurately calculate the everlasting option price we need to interpolate the data so we have maturities incremented on a continuous basis. In other words, we'll need to have price data for maturities across nearly 300 days (ie: 1, 2, 3, 4 .... 303 days left).
- We’ll also need the Deribit BTC index price on a daily basis to calculate the daily payoff of an everlasting option. This payoff value as will be discussed below is required to calculate the funding fee.
B. Model Implementation
We now have to think about how to aggregate all of this data into a singular everlasting option price. Because everlasting options did not exist over the sample period, we cannot refer to historical everlasting options prices. However, we can price their replicating portfolio, assume the everlasting options are always priced accordingly, and derive the appropriate funding fee from that.
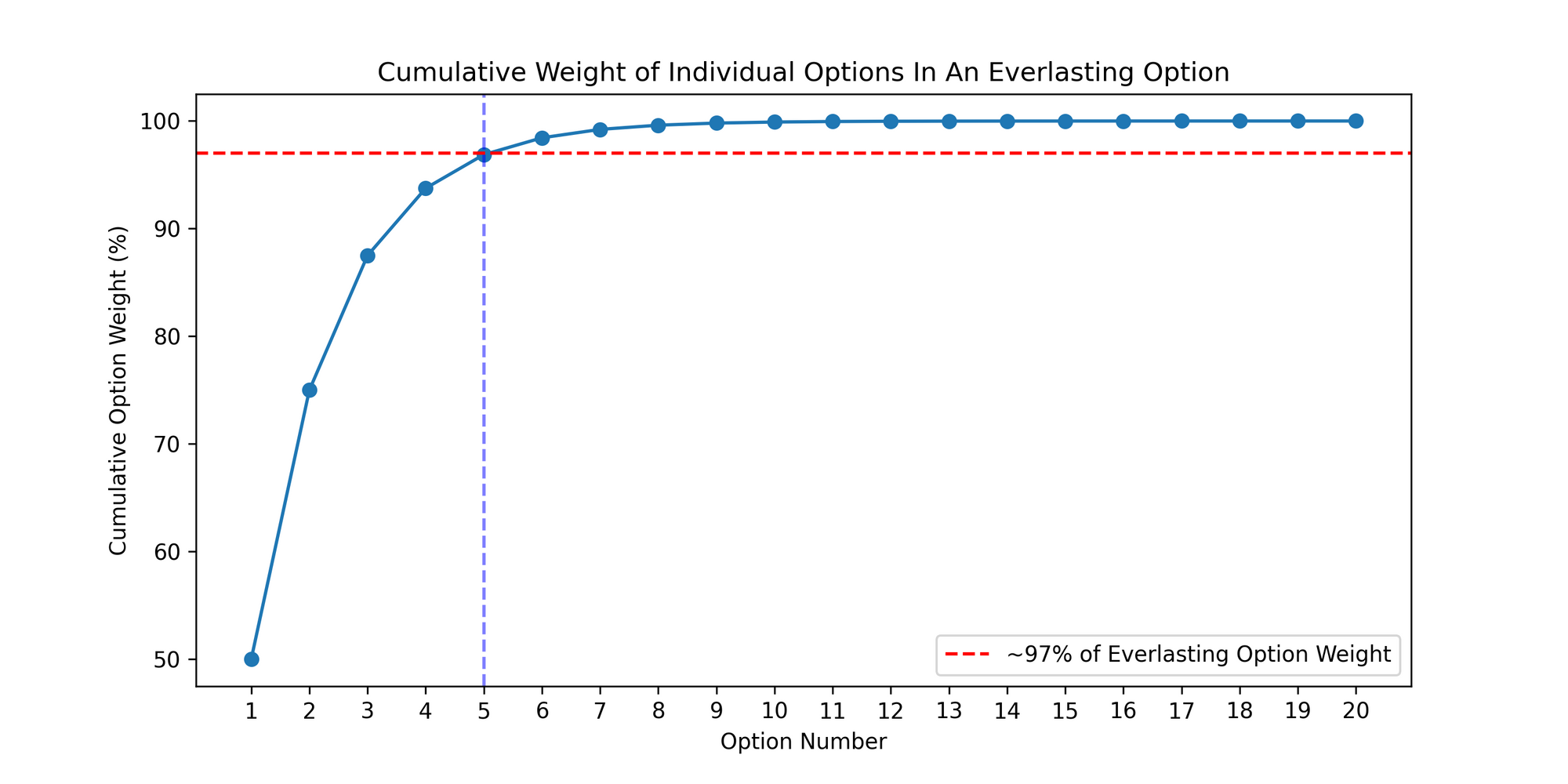
In the paper, each individual option was exponentially weighted in an arithmetic manner. For example, the 1 day option will make up roughly 50% of the everlasting price, the 2 day option will make up roughly 25% and so on.
Under this approach, nearly 97% of the everlasting option’s weighting will come from just the first five maturities. Therefore, the marginal impact past the fifth option should have a negligible impact on the overall everlasting option price.
From here we can proceed with calculating the price of the everlasting option for every day in the data, as well as the funding fee the longs would have had to pay to the shorts. Further details of the funding fee calculation can be found in the code accompanying this analysis.
C. Analysis of Everlasting Option Price and Funding Fee
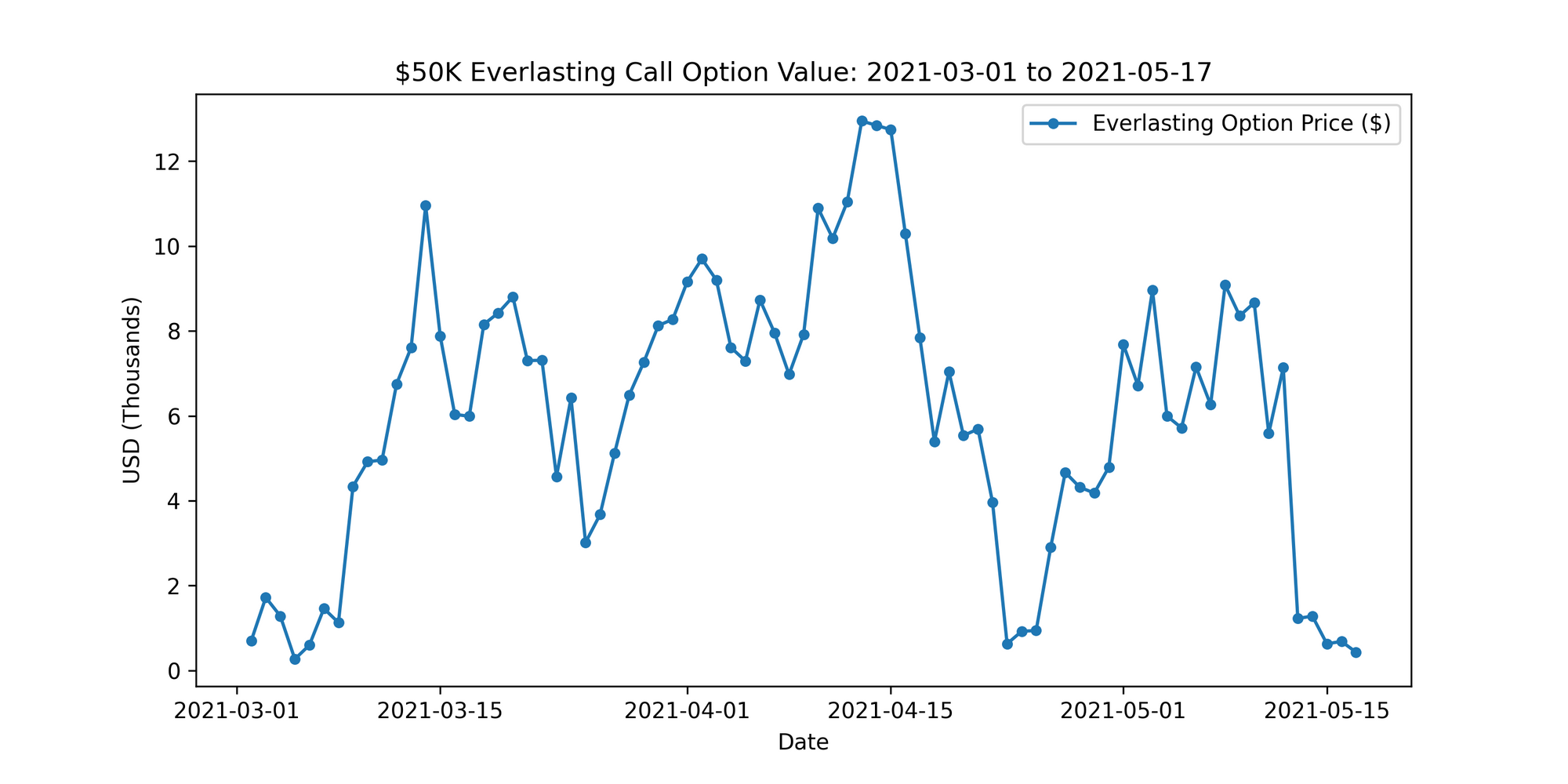
We now have a time-series output for both the $50k call everlasting option prices and the respective funding fees. At the start of the data, BTC was trading around $47k which means the everlasting call was slightly out of the money. A few weeks later, BTC climbed well past $50k to all time highs which was reflected by the massive spike in the everlasting option price, which was then far in the money. Similarly, the everlasting option price fell sharply amidst the bearish price action in April.
Dave brought up an insightful point that between 2021-03-01 to around 2021-04-15, the everlasting option traded similar to spot BTC. This makes sense because during this time the everlasting option was in-the-money which corresponds to a larger delta profile.
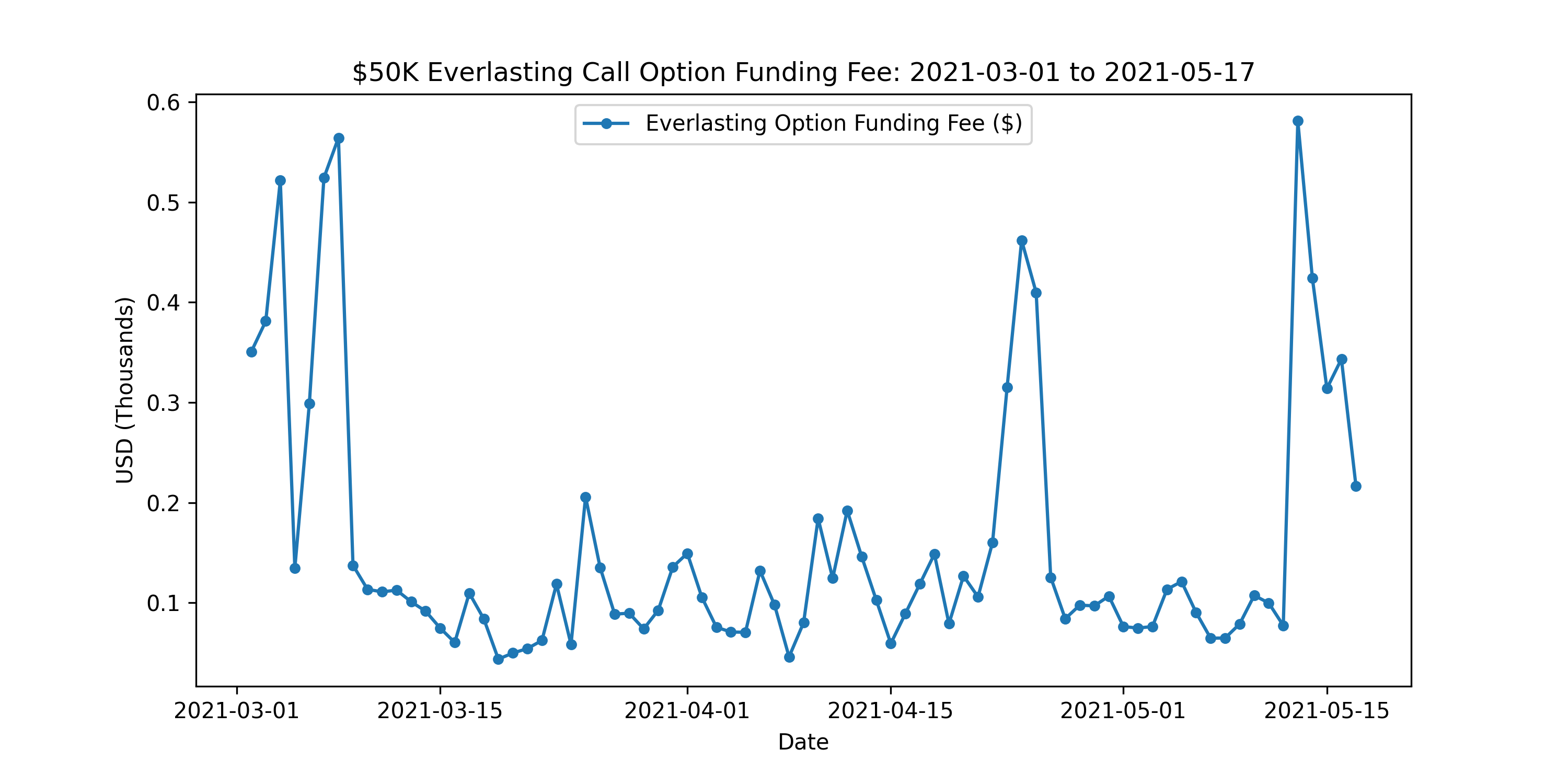
It was also interesting to analyze how the funding fee evolved over time. We can observe how the jump-like price behaviour in the everlasting options directly corresponds to similar changes in the funding fee. When the option is at the money, and has a lot of time value, funding fees are high. When it is deep in the money, funding fees are quite low, and should be almost identical to perpetual future funding fees.
Part 2: Theoretical Analysis of Volatility Shocks and Greeks
The goal of this analysis is to study the theoretical price behaviour for everlasting options in different volatility regimes while also analyzing the greeks. This can be useful for traders or market-makers to accurately assess the risk of buying or selling this product.
A. Analyze Impact of Volatility on Everlasting Options
In this example, we’re simply repricing a strip of 20 options and weighing their prices as discussed above. For example, let’s consider pricing a theoretical at-the-money $100 strike everlasting call option. The basket of 20 options that make up the majority of the replicating portfolio will be spaced out continuously with one day between each maturity (ie: 1, 2, 3, 4, … 20 day option).
With this approach we can now test out how the price of the everlasting option will behave when we shock various parameters. For this analysis we’ll focus exclusively on studying the relationship with volatility as it’s arguably the most important factor when pricing options.
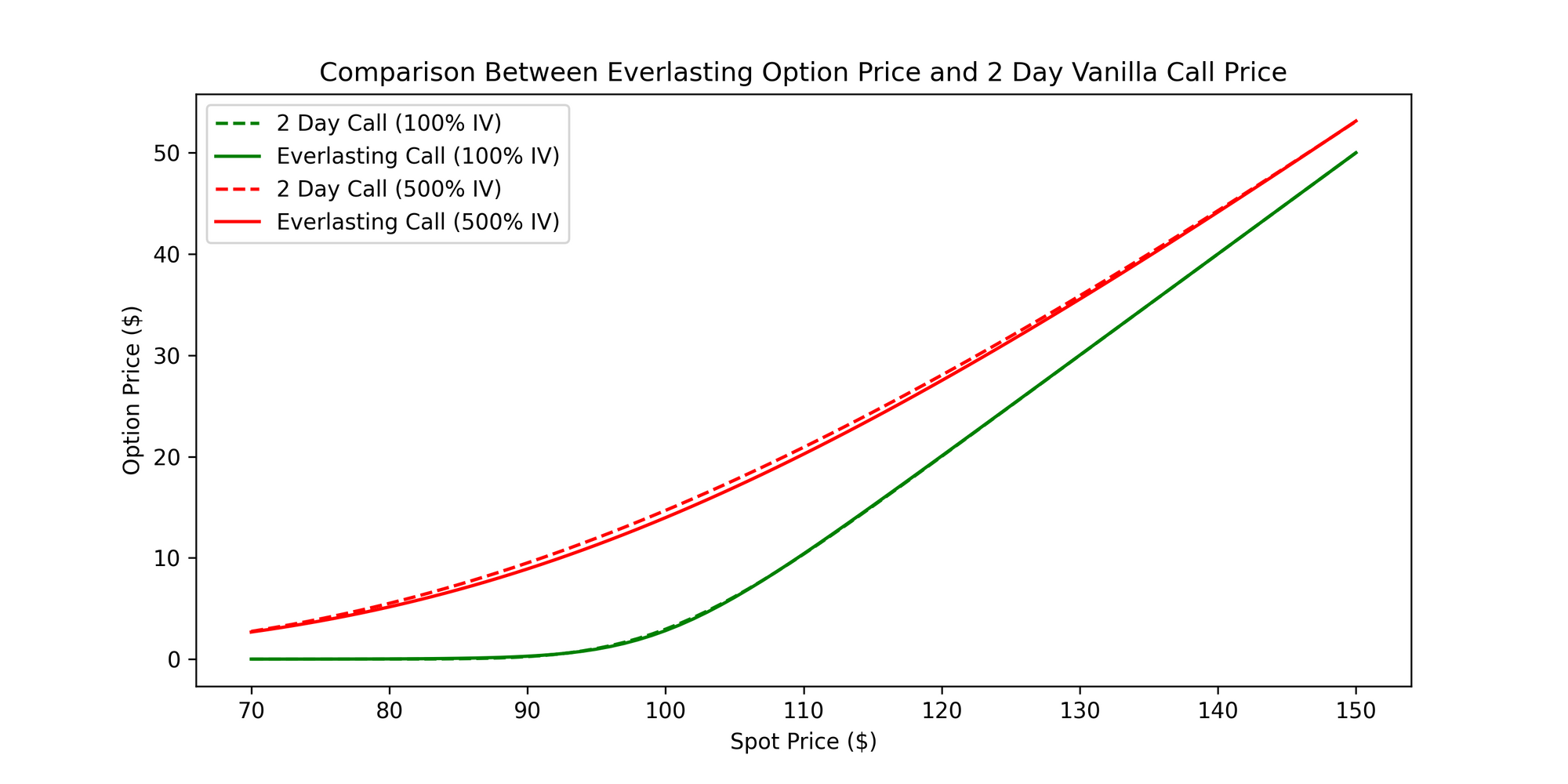
When we price both the everlasting and 2 day call option with 100% IV, the difference between the option prices is quite small (notice how the solid green line and dashed green line are close to each other). Similarly, when we price the same options with 500% IV, the difference between the option prices is still relatively similar.
In this example, we're assuming the funding fee is paid once a day. As a result, based on the math behind the everlasting options, the average time to expiry will be 2𝑁 where 𝑁 is how often the funding is paid. Therefore, if we're paying funding once per day, then the everlasting option would have an average time to expiry of two days (ie: 2 x 1 day = 2 days).
Although it’s highly unlikely that at-the-money IV will realize at 500%, even if it did, the difference in price between the 2 day call option and corresponding everlasting option (with funding paid on a daily basis) will be minimal. Overall, when we’re looking at strikes near at-the-money, periods of higher volatility do not correspond to larger differences between the everlasting option price and the corresponding 2 day option price.
B. Analyze Everlasting Option Greeks
Before trading any type of option, market-makers and traders must be able to understand their greek exposures. In the case of everlasting options, we’ll calculate the individual greeks for the first 20 options in the basket and weigh them under an exponential arithmetic average approach (similar to how we calculate the everlasting option price). It’s important to note that 20 is merely an estimate but captures nearly all of the dynamics of this option (in theory we could use an infinite number of options to construct an everlasting option).
In this example, we’re analyzing the greeks of an at-the-money everlasting option (Strike=$100, Spot=$100, IV=100% for all options). With this visualization we are able to see which greeks are most exposed to the first few options comprising the everlasting option.
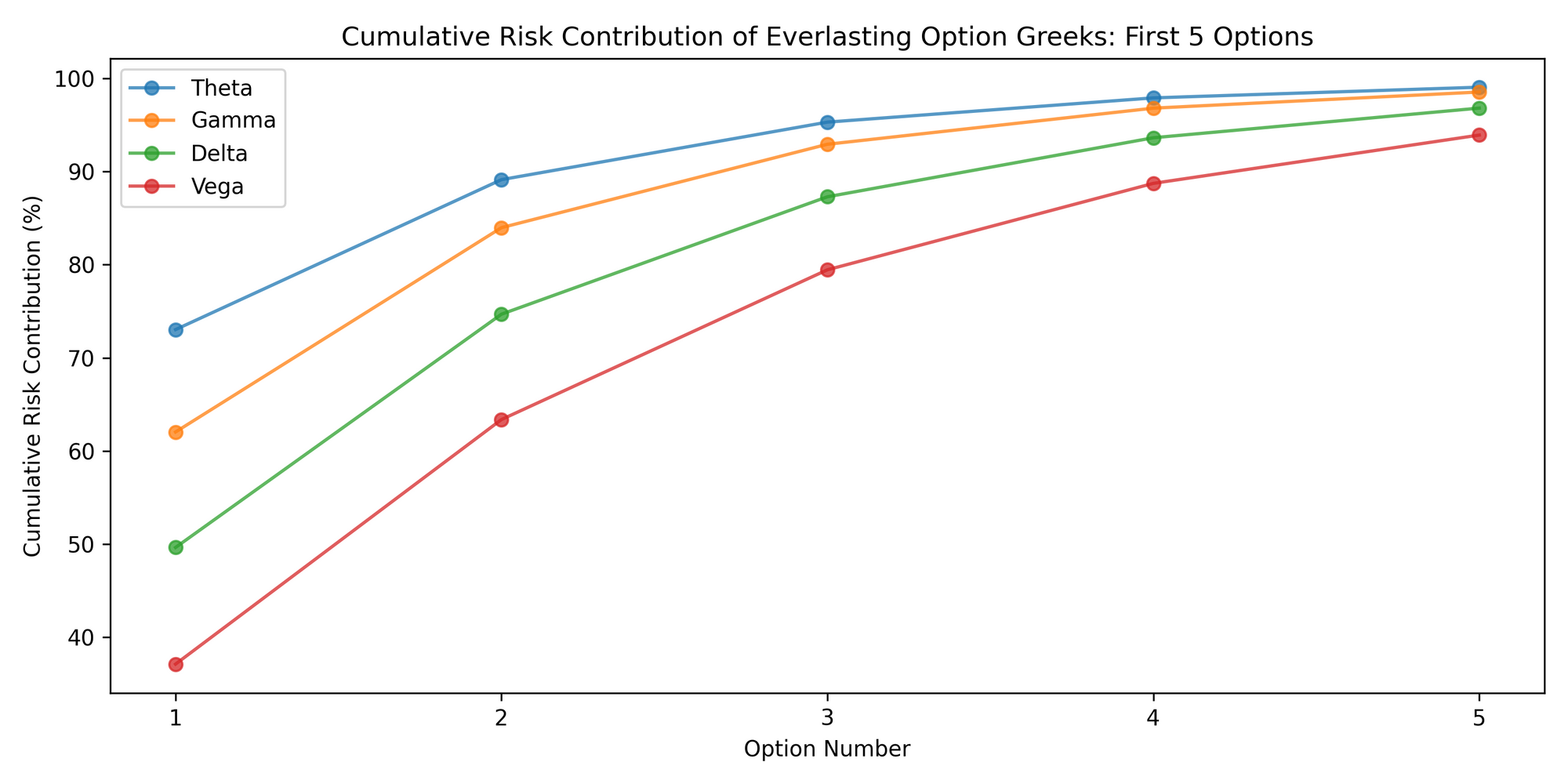
- Theta: Even though the one day call option has a weight of 50% in the everlasting option, roughly 70% of the total theta risk is concentrated in this single maturity. This makes intuitive sense because short-dated options tend to have very rapid time decay, hence the larger exposure to theta.
- Gamma: Roughly 60% of the everlasting option's gamma exposure comes from the daily option. This is similar to the discussion about theta as short-dated options tend to have large gamma exposures. It’s important to note this phenomenon is likely specific to at-the-money options given they have maximum gamma.
- Delta: Around 50% of the total everlasting option delta exposure comes from the one day option. This is probably because we're assuming constant implied volatility for all options which causes delta to be relatively similar across all maturities.
- Vega: Only 35% of the vega exposure for the everlasting option comes from the one day option. The reason for this could be because vega tends to be larger for longer-dated options (ie: short-dated options tend to have higher gamma whereas longer-dated options have higher vega). For this reason, longer-dated options are likely given more weight which causes the one day option to have less vega contribution.
Conclusion and Next Steps
Overall, it was an interesting exercise in analyzing the various characteristics of this new financial derivative. Everlasting options would in theory help reduce the liquidity fragmentation across different maturities which is a net positive for the market as a whole. However, given the extreme volatility in cryptocurrency markets, it’s hard to see liquidity staying in only a handful of strikes. For example, in our case we analyzed a $50k BTC everlasting call option, however, several days later this option was already in the money (ie: BTC price > $50k). In this case, the everlasting option would trade more like the underlying asset rather than the option. Given that in-the-money options have less optionality and are more capital intensive from a margin perspective, option traders would choose to trade strikes closer to at-the-money or out-of-the-money. Although traders won't have to worry about this option expiring, in this case they would have to constantly roll their positions into different strikes which nullifies one of the primary benefits of trading everlasting options.
As discussed in the paper, a potential solution to this problem would be to use floating strikes for the everlasting options. Floating options are exotic derivatives where the strike of the option is not fixed but rather it changes over time, and they can be adapted to be everlasting in exactly the same way as vanilla options. This will make the pricing of the option a little more interesting but would likely be the most realistic way for liquidity to stay concentrated in a single option. In other words, if there’s a single option which doesn’t expire and its strike adjusts corresponding to market behaviour, then there’s no need to have fixed strike everlasting options. For example, under a floating strike approach, traders could purchase everlasting call options where the strike is determined based on the past seven days exponential moving average price of BTC. With this approach, the strikes will dynamically adjust in real-time to converge to the current BTC price which can help traders avoid having to constantly trade into different strikes. In my opinion, this is the only way for everlasting options to gain mainstream popularity among both retail and institutional users.
Overall, everlasting options are an exciting new financial derivative which have the potential to drastically disrupt the overall cryptocurrency derivatives market. The benefit of maintaining perpetual options exposure without the need for constant expiration monitoring is a significant advantage which cannot be understated. Perhaps most importantly, with everlasting options at least option market-makers can also look forward to Friday just like everyone else.
Acknowledgements: Dave White for walking me through the theory of everlasting options and his extensive involvement in reviewing the code and written work for this research project. Ben Simon for encouraging me to turn this research project into a blog post. Joel John for helping me set up this blog and encouraging me to share my thoughts.
Disclaimer: Nothing mentioned in this article constitutes as financial advice. Opinions expressed are solely my own and do not express the views or opinions of LedgerPrime.